
Table of Contents
- GeT: A Pencil’s Finite and Infinite Games: Reflections after the GeT: Together at RUME Pre-Conference and Workshop by P. Herbst
- Reflections on My Experiences at the RUME 2023 Conference by Michaela Tracy
- GeTting Together in Omaha or My Trip to Omaha by Sharon Vestal
- Developing an Advanced Standpoint in Geometry for Teachers by Defining and Extending Objects across Geometries with their Connections and Justifications by Celil Ekici
- Embracing a Developmental Review Process: Fostering community and supporting contributors to the GeT Course Book by Amanda Brown
- Engaging with the Student Learning Objectives (ESLO) Working Group Update by Younggon Bae
- Transformations Working Group Update by Julia St. Goar
- Teaching GeT Working Group Update by Nathaniel Miller
- GeT to Know the Community: GeT: A Pencil community members and the GRIP Lab Staff at the GeT: Together at RUME meeting

GeT: A Pencil’s Finite and Infinite Games: Reflections After the GeT: Together at RUME Pre-Conference and Workshop
by P. Herbst
Our winter newsletter comes late this winter; it is officially spring! We wanted to wait until after our GeT: Together at RUME1 pre-conference and workshop to publish this issue. Indeed, I wanted to wait until after the conference to write this note, in part because it is somewhat of a spring time for GeT: A Pencil also. Valuable ideas are springing up, and we are looking for a way to support them so they can bear fruit.
Several of us were at our pre-conference and workshop on February 22 and 23, and though we missed some of you, the work of each of the three working groups was well represented. Moreover, we made much progress talking across the different teams writing chapters for the book on The GeT Course. After the conference, we have continued to orient author teams to each other, especially when we see chapter proposals possibly covering comparable ground. This move pursues two purposes that can be expressed in James Carse’s (1987) distinction of finite and infinite games. Finite games are like matches of a sport; they are played to the end and have a well defined result. Infinite games are like the sport itself; they are played in order to perpetuate the game. As games in a sport attest to, playing a game often involves playing both a finite and an infinite game. Such is the game of democracy, each election is a finite game, but democracy itself gets perpetuated each election.
Such is the case with our forthcoming book and the strategy to orient authors to each other. First, there is the finite game of writing and publishing the book, and to that end, we want to create mechanisms for each chapter to be unique. Along those lines, developing awareness of what others are writing is good for authors so that they can identify their chapter’s unique strengths and build on those. Second, and perhaps more importantly, there is the infinite (or, at least, indefinitely long) game of building and maintaining community around the GeT course to improve the teaching of geometry to future teachers. Writing and publishing the book and its chapters are a strategy to do that. The book is giving our community a chance to grow in numbers and to develop connections among members. In this sense, orienting authors to each other pursues the goal of building community and bringing more people in. I believe the pre-conference and workshop contributed to the playing of this infinite game as well. I want to revisit three reflections from these events that support the notion that beyond writing a book together, what we were doing was developing a stronger community.
First reflection: Developing narrative for GeT: A Pencil
In her reflections on the conference, Carolyn noted that one salient aspect for her was our collective realization of the need to develop and share a narrative of our community. It seems essential that, as we welcome new members, we can say more about where we are coming from and what we have been doing. Our concern with the geometry course for teachers is not the only defining aspect of our community; the way in which we are concerned with GeT courses also matters. Along those lines, the image of a pencil of lines2 might assist; the notion that we come to be involved with GeT courses from different directions (as lines that converge to the same point though they have different directions) is a key definitional idea. It helps, for example, to assert that the community is pluralistic, and not because we have not yet found “the truth” about how to improve geometry courses for teachers but because we do not surmise that there is such a thing to be found. Instead, we take the differences we bring as riches that can be combined into compromises and consensus positions. And we take the building of a community that accepts those differences as riches and commits to working with them as more important than hitting a single best idea.
In saying that, I am particularly aware of where I am coming from. As someone who does research in mathematics education, I have a particular way of looking at instruction that could be seen as the source of ideas on what “should” be done, but I do my best at second-guessing that instinct. I am willing to bring in information (e.g., what we know about the MKT-G test), ways of being in the world (e.g., creating, administering, and analyzing surveys is one way I know how to find things out), and some personal values (e.g., the aspiration that mathematics courses for teachers could improve prospective teachers’ knowledge of mathematics for teaching is something I believe is a valid concern) to our community. However, I am not willing to avail myself of the same prescriptive attitude many in the field of mathematics education take toward instructional practice and try to tell people what they should do. One thing we learn from research is that all the positive knowledge we may glean from research practice is eventually knowledge about models that reduce the complexity of real practice. There is quite a bit that researchers do not know, and the relationship between what is true and what should be done is always mediated by moral reasoning, on which researchers do not have a monopoly. Thus, I come to the GeT course also looking forward to learning from perspectives different from mine and not expecting that eventually people should think like I do.
I surmise that all our community members have a similar sense of what they know and can bring and also of what they do not know. Moreover, by coming to work together we are affirming some sense of interdependence, represented by the point to which all the lines converge; to make headway toward a common goal, the different lines need to find ways of getting closer to each other. Newcomers could be quite disruptive if they came across as someone who knows exactly what we need, and we might need tools to disabuse them of that thought without making them feel that we do not need them as participants or that what they have is not useful at all. Unfortunately, both the academy and the commercial world have conditioned us to expect that value is shown in the competition among products and that finding the best product is more important than how we find it. GeT: A Pencil has tried to do things differently, or maybe I should say, it has become a different kind of community, where the membership comes up with goals and means, and those are serviceable to maintaining and growing community where we look for complementarity among people and the riches they bring. I think we need good ways of impressing this aspect of our community onto others. Developing a narrative might help toward that.
The need for a narrative was apparent in at least two ways. One was in Dorin’s proposal that the book provide an account of how it is that we landed on the need to develop some essential Student Learning Objectives (SLOs). Dorin articulated the conjecture that each of the SLOs has a trace in our earlier activities mapping the courses that each member of the community has been offering. This mapping exercise happened during our first year. We started with a map that I created where I tried to be inclusive of all sorts of things I had heard in our interviews, seen in the posters at the 2018 conference in Ann Arbor, or learned from research. I did that in a piece of software that allowed people to create their own mind map by editing the original mind map. It seems that the software was handy for people to subtract nodes and add new nodes as needed, and a nice set of very diverse maps was created. I was not at the discussions of those diverse maps, but what I heard was that out of that diversity came the impetus to develop the set of SLOs.
The second way in which the need for a narrative was apparent was in Erin’s advocacy that the complete set of elaborations on the SLOs should be included in the book. This seemed like a good idea to everyone I have talked to, especially because the book is being written in response to the current version of the SLOs, and so, having the current version in a place from where it can be cited seems really important. At the same time, part of the narrative about the SLOs is that they are a living document, and their existence on the website getapencil.org means to keep track of that living document over time (i.e., the site will archive old versions and post the newest version of the SLOs). It seems to me that the publication of the first version in the book is akin to the photo with which we often introduce a new family member to our acquaintances. As the child grows, new photos document what they look like, but old photos are still valuable to tell the life story. With this, I mean to say that for the SLOs to actually be a living document, we might need to embrace the idea that we will have periodic releases, comparable to an annual school portrait of a child. The first picture may be the publication in the book, and subsequent ones might be on the website or in other books that may emerge later on. They will all help us tell the story of how the SLOs exist as a living document.
Second reflection: How does the living document continue?
A second reflection was about possible mechanisms to keep alive the discussion of SLOs as we enlarge the community. As I mentioned above, all three working groups were represented at the conference. One of the three groups, the ESLO group, represented by Michaela, Younggon, and Mara, has been meeting since October 2022 and includes both mathematics professors and secondary teachers. The acronym ESLO means Engaging with the Student Learning Objectives, and the group’s finite game is to provide a first set of commentaries on each of the SLOs. By the time of the conference, the group had managed to discuss only the first three SLOs and had not posted any commentaries on the website yet. However, it was already clear that they had things to say that could inspire changes in the SLOs. We heard, for example, that the current version of SLO 3, while oriented to meeting the content needs of high school geometry, had been written in such a way that it only covered process standards. The ESLO group was not satisfied with that.
The ESLO group had been having discussions of how particularly rich tasks could be used in GeT courses to bring up some of the content from high school geometry. I had been thinking about that too. In my own work teaching future secondary teachers, I have often used the angle bisectors of a quadrilateral task (to answer the question “what can be said about the angle bisectors of a quadrilateral?”) in teaching them instructional methods. This task has a lot of rich mathematical content that connects to several of the topics and processes of high school geometry. The question itself calls for reviewing what an angle bisector and a quadrilateral are. Considerations of what sorts of things could be said arise from tinkering with incidence questions (e.g., how many intersections can be created with 4 different lines?). An interesting contrast is often recalled with triangles where the angle bisectors always meet at a pointa; and one might then ask in what circumstances the angle bisectors of a quadrilateral do so. But one might also ask what figure do the intersection of the angle bisectors make when they don’t converge at a single point. All of that questioning makes good use of concepts of parallelism and congruence, the sum of the angles of a triangle and a quadrilateral, and properties of tangents to circles. The ESLO group discussed other tasks that might be used to review the high school geometry content.
In response to the brief feedback on SLO 3 provided at the conference, we heard back from the Teaching GeT group that SLO 3 had a rocky history and that even the original writing team was not completely sold on its current state. Out of this exchange came the thought that two new chapters in the book could help represent how the revision process will come about. In one of these chapters, members of the ESLO working group will articulate their critiques of the current version of SLO 3, and in the other chapter, members of the Teaching GeT group will respond, possibly with a proposal for a new version of SLO 3. Including this exchange in the book might help show the community at large how the living document idea could be brought to fruition. It will not just be a matter of adding or subtracting from the original document; it will take engagement with the prior work and incremental improvement upon it. This process illustrates the infinite game of community building.
How the community continues to exist
Amanda and I sometimes describe the development work we do in our projects (including GeT Support and ThEMaT IV and V) as soft professional development. We see ourselves as creating facilities (environments, tools, events) that allow people to learn through doing work together. Often, over time, change happens organically, but we do not see ourselves as leading anybody to make any particular change; we treasure, instead, the opportunity to build communities from which people will draw the support to do what makes sense to them. Because of this, I have a love/hate relationship with the expression professional development. On one hand, the expression is handy to put our work in a box and in the company of other projects. On the other hand, that company sometimes generates expectations that are unlikely to be the ones I would like to accept responsibility for. The latter includes the “I am trying to make you change” sort of stance toward participants; I try not to come across that way. The work I do is very unlike professional development, in the sense that there are no specified changes I pursue for the community to enact, and I do not consider myself an expert on what the community is or should be doing. Along those lines, I am really happy about how much we have been able to do together cooperatively and collaboratively.
The word cooperation is often used to describe people doing things in parallel while making use of common resources. An example of this is how the work of the working groups occurs in parallel while the GeT Support project provides resources such as recordings and publication on the website and the Newsletter. The GRIP Lab also benefits from those resources in that, as some of you may have seen at RUME, one thing we are doing in our analyses of the transcripts from working group meetings is to investigate how the consensus develops. As you may surmise, the arguments that happen around instructional decisions are different than mathematical arguments; they include mathematical considerations but also other considerations, and they draw from the variety of funds of knowledge that members bring with them (in all cases the working groups include mathematicians and mathematics educators; ESLO also includes teachers with experience teaching high school geometry). We also are able to further our work documenting the teaching of geometry for secondary teachers when community members distribute our surveys and MKT-G tests. It has been great to see that side projects such as the Adinkra lesson study group or the study of using the FullProof software have developed around subgroups from within the community. At the RUME conference we could also attend each other’s presentations and learn about each other’s work.
The word collaboration is often used for a different kind of joint work–not the sharing of the same resources and working in parallel but rather working together toward a common goal. The various writing projects we have done together illustrate this aspect of the community’s work. Sometimes we have the chance to coalesce into a single task. The book chapters we wrote recently and the forthcoming book illustrate this collaboration. Along those lines, I was happy to hear the warm reception of my idea of dedicating part of the new grant proposal to the development of an “uber-book” that includes tasks, videos, dynamic geometry sketches, and more, using an electronic book platform that permits user research. I think if we do get funded it will give us a great opportunity to collaborate. As we move closer to writing a new grant to support the community for another four or five years, it will be great to hear what other projects members would like to engage in to also sustain cooperative work.
Conclusion
We are by no means done yet, but I can say that the work of GeT Support, developing GeT: A Pencil as a community has been a highlight of my career. But it is only spring! We can look ahead to milestones in the production of the GeT Book as a finite game. Receiving the chapter submissions at the end of May will be like half-time break, and then, after feedback and editing, we can look forward to the end of that finite game. But the infinite game of growing the community will continue. Keeping our narrative in mind, whereby it is not just the goal of improving capacity for high school geometry instruction but the pluralistic way in which we go about it, will be important. I surely hope more people will join us in our cooperative and collaborative work.
References
Carse, J. (1987). Finite and infinite games. Ballantine.
_________________________
1NB: RUME is the annual conference of the Special Interest Group on Research in Undergraduate Mathematics Education of the Mathematical Association of America. See http://sigmaa.maa.org/rume
2A pencil of lines is the set of all lines that shares a common point.
Suggested Citation
Herbst, P. (2023, April). GeT: A Pencil’s Finite and Infinite Games: Reflections After the GeT: Together at RUME Pre-Conference and Workshop. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#get-a-pencils-finite-and-infinite-games-reflections-after-the-get-together-at-rume-pre-conference-and-workshop

Reflections on My Experiences at the RUME 2023 Conference
by Michaela Tracy
I was delighted to be invited to join the GeT community in Omaha this past February. As a high school teacher, this was my first time attending this type of gathering. Also, because I work in Massachusetts, I have not had the opportunity to attend local events in Michigan before. At first, I was worried that I might feel out of place, especially as the only K-12 educator at the conference. However, I was immediately and warmly welcomed by the entire GeT community. I was encouraged to participate fully and share my unique perspective as a high school educator. While my day-to-day context differs a lot from the majority of the people I spoke with, everyone shared a common goal: improving the capacity for teaching geometry. It was refreshing to learn about the unique experiences from the GeT instructors I met with throughout the conference.
In terms of the work around geometry, I attended the GeT Together pre-conference meeting on Wednesday, February 22 and the RUME working group the next morning. I found the work at the GeT Together so enlightening and impactful. I am currently a member of the ESLO working group. As members of that working group, we are tasked with providing feedback about the SLOs to the original authoring group. We have been meeting bimonthly since October, and so far, we have engaged mostly with the first four SLOs. Even though we are not yet finished exploring all the SLOs in detail, it has been great to engage with high school teachers and college instructors about the SLOs and secondary geometry in general.

My biggest takeaway was that it was fantastic to finally meet in person. This conference was the first time I met members of the ESLO group. I had also worked with some people in attendance a while back on some of the Lesson Sketch work. It was great to actually talk with people I have been on Zoom with for years! I was also able to meet the members of the original SLO authoring team. Being able to interact, share meals, and connect with these instructors made the work seem not only more personal, but also more enjoyable. I was able to gain valuable background information about the original formation of the SLOs and learn more about the struggles and difficulties the authors faced in the process of constructing the SLOs and the elaborations that complement them.
Our work on Wednesday focused on what the GeT community has been working on. We also had time to connect about our chapters for the upcoming book. My authoring group had time to connect with another group, and ultimately, we decided to combine our efforts into one chapter. This time to connect and collaborate was critical in helping us all move forward with our writing. At the end of the day, we talked about what work we want our community to focus on in the future. I was really heartened to hear how much college instructors care about geometry. From the high school level, it always feels like geometry is the area we are trying to deemphasize. Due to time constraints and the loss of learning from the pandemic, we have cut a lot of geometry content from my school’s curriculum. While this loss is unfortunate, I left Wednesday’s meeting reinvigorated to promote the teaching of geometry in my school. Equipped with research, connections to university faculty, and arguments to help defend geometry teaching, I am hopeful my learning on Wednesday will lead to positive change in my school community.
Thursday’s working group was open to the entire RUME conference, and we had a few people join us from outside the GeT community. We broke up into groups and looked at how we can further the work of the SLO team. My small group worked on brainstorming potential areas of research to advance the scholarship around the SLOs. I enjoyed talking with three college instructors, learning more about the types of students they work with, which include pre-service teachers. I was able to share experiences from my own time as a pre-service teacher and think about experiences that would benefit that group of people.
Overall, I left Omaha thinking deeply about how I can work as a high school teacher to advance the teaching of geometry in my own school. I brought back some tools, including some of the software and resources the GeT instructors showed me throughout the week. At the ESLO meetings since my trip, I have felt a stronger connection to our work and the community at large. I look forward to meeting with the GeT community more in the coming months and years, and I am appreciative to be a member of this community.
Suggested Citation
Tracy, M. (2023, April). Reflections on My Experience at the RUME 2023 Conference. GeT: The News!, (4)2. https://www.gripumich.org/https://www.gripumich.org/v4-i2-wi2023/#reflections-on-my-experiences-at-the-rume-2023-conference

GeTting Together in Omaha or My Trip to Omaha
by Sharon Vestal
When I found out that the RUME conference was going to be in Omaha, I was probably the only member of the GeT: A Pencil group who was excited. For me, it was a 4-hour, 235-mile trip down Interstate 29. The Embassy Suites was the perfect venue, located within walking distance of several restaurants, with a friendly staff, and a great evening happy hour! Many of us from the GeT group spent a lot of time visiting with each other during these happy hours.
The GeT Together on Wednesday started around 9 a.m. with a welcome from Pat. Then Laura and Amanda updated us on the book, and we got to see a list of accepted chapters. It was valuable to all of us that are writing chapters to see what others are writing. Then Dorin talked about his proposed chapter on the archetype work that we did in 2018-2019. I do believe that work was instrumental in getting us to the GeT Student Learning Objectives (SLOs) so I am thankful that he has gathered a team to write that chapter. Michaela from the ESLO group shared what they have been doing and some of their thoughts after discussing the first three SLOs. Engaging with Michaela, Mara, and Younggon from the ESLO group was nice. I appreciated hearing their perspective on the SLOs, especially Mara’s sharing on how she has changed her GeT course and feels that the course has improved with the addition of the SLOs.
The opportunity to split into different groups and talk about the proposed chapters in the afternoon was very useful. When you are meeting with your co-authors, everyone often has a similar perspective so getting ideas from an outside person was helpful. I think that some of the author teams made progress on their chapters. Thanks to Inese and Carolyn for all they did to organize and keep us on task!
During the Thursday morning RUME Teaching Geometry for Secondary Teachers working group, we were joined by a couple of new people interested in the GeT course. Nat started us off by showing the SLO website. We are still hoping that more people register for the Forum and share their thoughts on the SLOs there. If people join the forum and leave comments there, anyone registered for the forum can read their comments and respond.
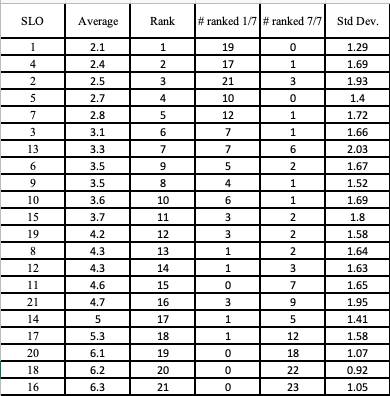
Then Mike presented the results of a survey done by the GRIP lab, where they listed the ten SLOs, along with eleven distractor SLOs, and people had to rank them 1 through 7. The survey results are in the image at right. These survey results were very satisfying for me (and likely others in the SLO authoring team). Nine SLOs were ranked in the top ten slots. Notice that SLOs 1, 4, 2, 5, and 7 were ranked #1 at least ten times. In addition, all of the SLOs had very few #7 rankings, with SLO 2 having the most with three rankings at #7. While SLO 8 is lower in the rankings, it was only ranked #7 twice. SLO 13 was “Understand the ideas underlying advanced geometric topics in Euclidean and absolute geometry.” I feel like these survey results solidify that we were on the right track in selecting and writing the SLOs.
Thursday afternoon I was able to see some of my GeT colleagues present about the Adinkra lesson that they have been using to teach transformations in their courses. It is always great to support other colleagues in their teaching and research. In addition, Tuyin, Orly, and I presented our FullProof project, including data from both fall semesters that we have used it. While we had done a similar presentation at AMTE in New Orleans, this one had better attendance and audience interaction. The best part was seeing our GeT colleagues in the audience supporting us and asking questions.
As a first-time attendee of RUME, I really enjoyed it. I teach the proof course at SDState so I was able to find a lot of great sessions on teaching and learning proof. Another thing that I liked about it was that it is a smaller conference, so everyone knows each other. Dinner with the GeT: A Pencil community on Thursday evening was a lot of fun. Our table was lucky enough to have Joe Cole, the magician comedian, come and show us one of his tricks. The best part of my trip to Omaha was hanging out with the GeT: A Pencil community—what an awesome group of people. This community has been wonderful for me professionally, and I have also found amazing and supportive friends!

Suggested Citation
Vestal, S. (2023, April). GeTting Together in Omaha or My Trip to Omaha. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#getting-together-in-omaha-or-my-trip-to-omaha

Developing an Advanced Standpoint in Geometry for Teachers by Defining and Extending Objects across Geometries with their Connections and Justifications
by Celil Ekici
Abstract
In this article, I propose a reconsideration of mathematical content for teaching high school geometry for preservice teacher education based on my own experience teaching geometry courses. The Conference Board report on the mathematical preparation of teachers recommended that future teachers complete three courses focused on school mathematics from an advanced viewpoint (CBMS, 2012). As regards to geometry, they argued that preservice teachers’ preparation should enable them to stand above the content of high school geometry. Kilpatrick (2019) brought to the attention what Felix Klein had called the double discontinuity between university-to-school mathematics and the triple approach Klein had proposed to address it by a unified approach to show how problems in branches of mathematics are connected (e.g., geometry, algebra) and how they are related to the problems of school mathematics. As defined by Klein (2004) and Usiskin, Peressini, Marchisotto, and Stanley (2003), an advanced standpoint on geometry can be developed by focusing on alternative definitions of familiar geometric objects, their extensions, and connections. Here I present my experience conducting classroom experiments on developing an advanced perspective for future teachers exemplifying ways to revamp College Geometry courses preparing future teachers to teach high school geometry.
Here, an advanced standpoint is built by unifying three strands, each of which consists of activities involving the making of connections towards developing a more unified perspective about the geometry content teachers are teaching. The three unifying strands are 1. connections within geometry, 2. connections between geometry and other subjects, and 3. connections between the alternative perspectives on proof and justification practices in geometry. The first strand of activities explores the connections within geometries. Adopting an inquiry-based approach to learning geometry courses, familiar geometrical objects, such as square, rhombus, or parabola, are reconsidered in different geometries with their defining properties and relationships. Students are asked to consider how we can define a geometric object so that once we translate the definition into another geometry, such as hyperbolic, it will still hold. The first set of bridging task sequences builds an inquiry into extensibility of definitions of familiar geometric objects such as quadrilaterals and parabolas across Euclidean and non-Euclidean geometries. Students develop the family relationships among quadrilaterals in different geometries based on their definitions.
The extensibility of geometric objects, such as rhombus or parabola, across Euclidean and non-Euclidean geometries is investigated to gain a higher standpoint. Teachers explore whether the definitions of geometric objects are extensible by exploring what their definitions would generate in alternative geometries. They discover that rhombus is a shared parent object for equilateral quadrilaterals subsuming squares in Euclidean and quasi-squares in spherical and hyperbolic geometries. In all three geometries, they observe that rhombi have diagonals that are perpendicular and bisect each other. Students use this property as a defining characteristic of squares/quasi-squares in Euclidean and Non-Euclidean geometries. An extensible definition of a square is therefore developed across alternative geometries reconceiving the square as a rhombus with congruent diagonals (See Fig 1).
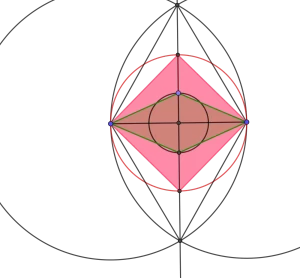
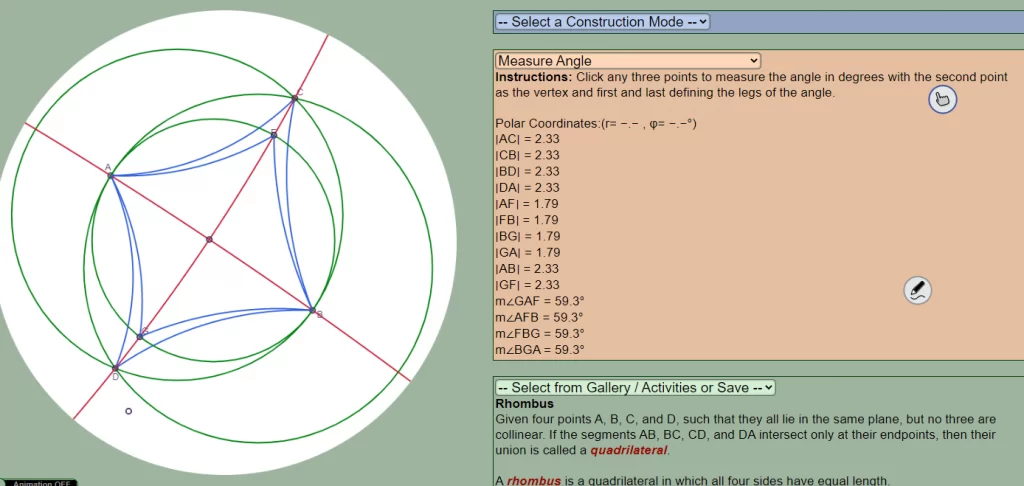
Figure 1. Quasi-Squares from rhombus as equilateral quadrilaterals with congruent diagonals extensible to Hyperbolic and Spherical Geometries
Students gain a higher perspective by revising a familiar geometric object in alternative geometries and acquire new meanings for that object by extending the geometric object into other geometries, redefining it through its viable manifestations. The various definitions of parabola are discussed as a case of defining a common geometric object by employing their constructive protocols to consistently build and contrast the features of the produced objects across geometries. Extensibility of the transformation approach from Euclidean into other geometries is discussed by recontextualizing the practice of isometries, symmetries, and dilations in Spherical, Hyperbolic, and other geometries.
The second sequence of bridging tasks involves connections across geometry, statistics, and irrational numbers. I introduce future teachers to dual modeling task sequences in which they model a common problem, first using a geometric approach and then using another approach, such as statistics. The classroom experiments presented here build a scholarship of teaching and learning mathematics over three years, deliberately modifying and revising the targeted instructional tasks across three classes regularly taught by the author. I do this in various courses including College Geometry (for secondary mathematics teachers), Fundamentals of Mathematics II (Proportional Reasoning, Statistics and Probability), and Fundamentals of Mathematics III (which is a Geometry course for Elementary and Middle Grades Mathematics Teachers). I design, assess, and revise local instructional theories to help to coordinate students’ modeling work and actions across the multiplicity of these mathematical frames. This helps future teachers develop coherent meanings across fields, such as geometry and statistics building on proportional reasoning. In an inquiry-oriented instructional setting, students are intended to discover the mathematics behind modeling stars mainly by statistical and geometric perspectives. In geometrical modeling, students construct pentagons first by using GeoGebra’s given construction and then create the corresponding pentagrams as stars by connecting the diagonals. Students discover the similarity of triangles DAB, ABH, and BHI with a golden proportion as the similarity ratio as seen in Figure 2a below. Then students build their own constructions of pentagons and stars by creating segments with golden proportion as seen in Figure 2b. In statistical modeling, students produce 24 hand-drawn pentagrams as best as they can. Students then measure and find the proportion of the average arm lengths and average distances between the vertices for each star. Students discover that the distribution of these proportions yields the median of 1.617, which is a close approximation to golden ratio. This approach is designed to offer students opportunities to build connections and develop coherent meanings with the geometrical and statistical patterns that emerge in modeling starlike objects.
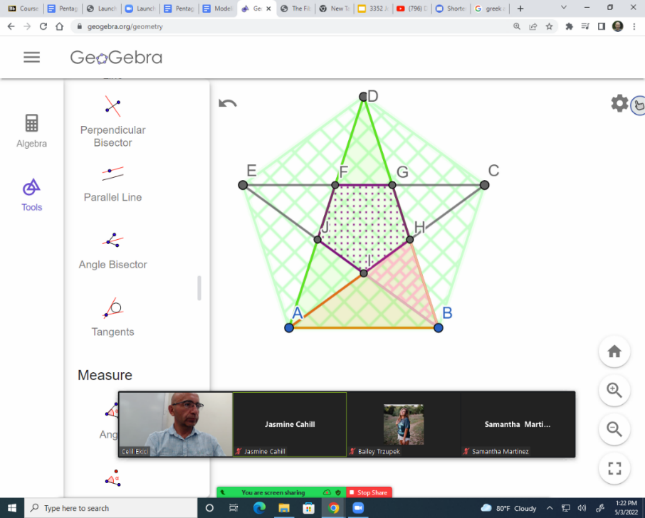
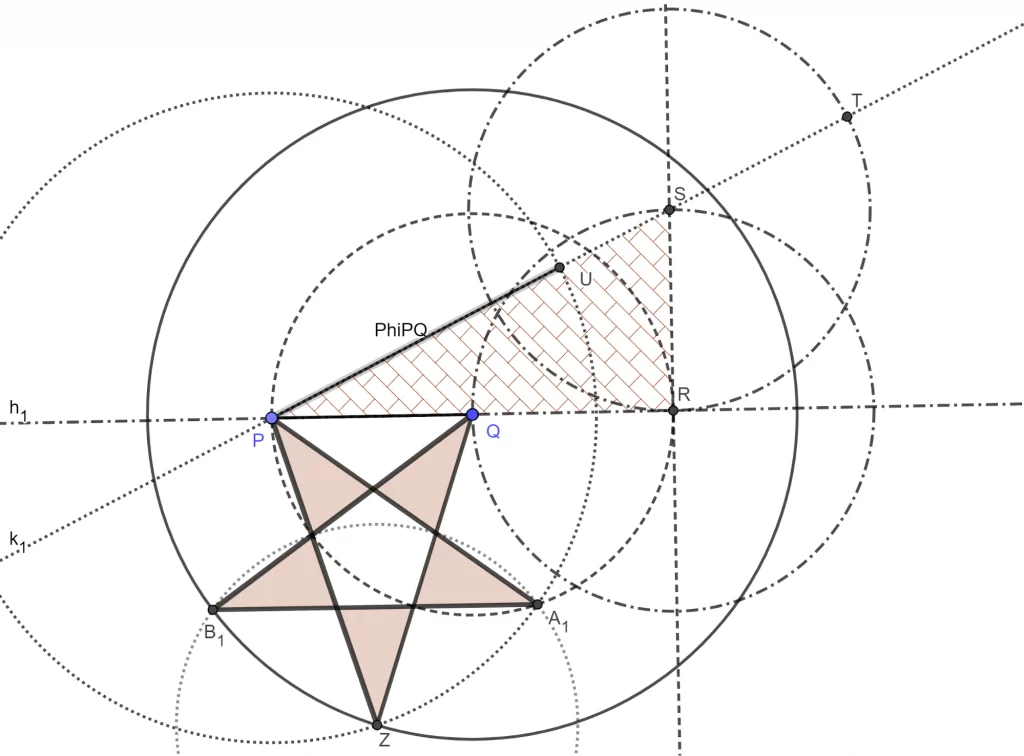
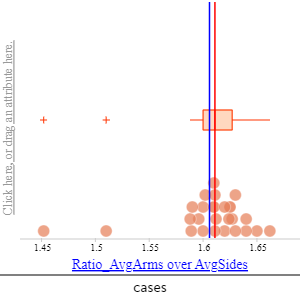
Figure 2. (a) Discovering golden proportions by connecting the Golden Star, pentagon, and golden triangles using the golden ratio; (b) constructing pentagram from golden proportions; (c) Statistical modeling of a star with a discovery of 1.617 from the distribution of the ratios of average arms over average side across 24 imperfect stars drawn by students
The third sequence of bridging tasks is about contrasting geometric arguments based on the standpoints of different axiomatic systems such as Euclid’s, Hilbert’s, and SMSG’s (School Mathematics Study Group 1961) and transformational approach. Students investigate and compare the justifications of their arguments as they conjecture, build, justify and validate arguments by creating versions of their theorems and proofs from different standpoints including a transformational approach. Future teachers adjust the level of rigor and justification of the arguments they offer or expect from middle and high school students.
This paper illustrates the use of three unifying strands for teaching geometry by building an advanced standpoint in geometry for preservice teachers, providing a more unified approach to geometry practice integrating with other disciplines.
References
Kilpatrick, J. (2019). A double discontinuity and a triple approach: Felix Klein’s perspective on mathematics teacher education. In H.-G. Weigand et al. (eds.), The Legacy of Felix Klein, ICME-13 Monographs, (pp.215-226). Springer. https://doi.org/10.1007/978-3-319-99386-7_15
Klein, F. (2004). Elementary mathematics from an advanced standpoint: Geometry. Mineola, NY: Dover Publications
Matsuzaki, A., & Saeki, A. (2013). Evidence of a Dual Modelling Cycle: Through a Teaching Practice Example for Pre-service Teachers. In G. Stillman, G. Kaiser, W. Blum, & J. Brown (Eds.), Teaching mathematical modelling: Connecting to research and practice (pp. 195–205). New York: Springer.
Usiskin, Z, Peressini, A., Marchisotto, E., & Stanley, D. (2003). Mathematics for high school teachers: An advanced perspective. New York: Prentice Hall.
School Mathematics Study Group (SMSG). (1961). Geometry. Yale Univ Press.
Suggested Citation
Ekici, C. (2023, April). Developing an Advanced Standpoint in Geometry for Teachers by Defining and Extending Objects across Geometries with their Connections and Justifications. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#developing-an-advanced-standpoint-in-geometry-for-teachers-by-defining-and-extending-objects-across-geometries-with-their-connections-and-justifications

Embracing a Developmental Review Process: Fostering community and supporting contributors to the GeT Course Book
by Amanda Brown
I am excited to be writing to you with an update about the upcoming book entitled The GeT Course: Resources and Objectives for the Geometry Courses for Teachers. Since the RUME conference, the co-editor team has been busy finalizing the review criteria for the submissions that are due in May. At the conference, some of you shared concerns you had about the review process, including worries about what kind of review criteria might be used for handling such a diverse group of authors, as well as the need for rigorous criteria to ensure quality contributions. We want to assure you that we have taken these concerns into account and have developed a set of developmental review criteria that will encourage reviewers to provide feedback that not only assesses the quality of the contribution but also aims to support contributors’ professional growth.
We recognize that the authors of this book come from diverse backgrounds and may have different standards for peer review. Writing for such a diverse audience may make the review process feel intimidating for some. We do not want it to feel that way. Our hope is that the review criteria supports the kinds of interactions that give all our contributors a learning opportunity to improve their writing for a more diverse audience and creates a book that embraces the diversity of our community. To construct the review criteria, the editorial team has drawn inspiration from several sources, including the review criteria from popular journals such as PRIMUS and Mathematics Teacher Educator which aim to support individuals engaged in teaching teachers in undergraduate mathematics and teacher education courses. We have also paid particular attention to developing criteria that encourage reviewers to produce what Sandra Crespo, a former editor of Mathematics Teacher Educator, has called an educative rather than evaluative review. With that, we thought we could use this opportunity to share a bit more about what we mean by terms like a developmental or educative review.
The idea of an developmental or educative review is not a new one. Peter Elbow, an English professor who devoted his career to democratizing writing, argued for the need for a more balanced approach to the review of academic writing. Elbow (2000) noted that as part of our training as academics, we are trained to take a critical stance toward new ideas—being as analytical and skeptical as possible. He called this the doubting game. Without discounting the importance of this kind of training, he advocated for the importance of embracing a different kind of stance towards new ideas—one that he called the believing game. In contrast to the doubting game, Elbow described the believing game as the “disciplined practice of trying to be as welcoming or accepting as possible to every idea we encounter: Not just listening to views different from our own and holding back from arguing with them… but actually trying to believe them” (Elbow, 2008, p. 2). He argued this kind of disposition as useful because in order to validly assess an new idea, even if we ultimately reject it, we must first dwell in it, really endeavoring to understand it, believe it, and see it from the viewpoint of the one who is offering the idea. Furthermore, if we only play the doubting game with other’s ideas, we run the risk of missing “what’s good in someone else’s idea” (ibid).
For our own purposes, embracing the believing game has value beyond helping us, as individuals, better assess the merit of new ideas. The believing game is also highly consistent with the values that have been part of GeT: A Pencil from the beginning—values which have supported the gathering of a community of individuals drawn from a variety of backgrounds to support one another and help each other grow professionally while working together to improve the capacity for teaching high school geometry.
With this focus on the believing game, we have specified criteria intended to encourage reviewers to provide specific, constructive, and actionable feedback, highlighting strengths and opportunities for improvement in a way that helps authors to move forward. This mirrors the kind of feedback we have seen so many of you provide as you have walked through the difficult conversations about GeT courses that have informed the first version of the GeT SLOs.
We look forward to sharing more specific details about the review process soon, and we invite all of you to join us in this exciting endeavor of engaging in a process of review that not only worries about improving the book’s contributions but also endeavors to continue expanding our community of support for individuals that have taken the risk to contribute a chapter for the book and count themselves as among the stewards for the undergraduate geometry course for teaching. Together, through our efforts in this review process, we can create a resource that supports the teaching and learning of geometry for teachers across a wide range of settings and experiences.
References
Crespo, S. (Ed.). (2016). EDITORIAL Is It Educative? The Importance of Reviewers’ Feedback. Mathematics Teacher Educator, 4(2), 122-125.
Elbow, P. (2009). The believing game or methodological believing. Journal for the Assembly for Expanded Perspectives on Learning, 14(3), 1.
Elbow, P. (2000). Everyone can write: Essays toward a hopeful theory of writing and teaching writing. Oxford University Press on Demand.
Suggested Citation
Brown, A. (2023, April). Embracing a Developmental Review Process: Fostering community and supporting contributions to the GeT Course Book. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#embracing-a-developmental-review-process-fostering-community-and-supporting-contributors-to-the-get-course-book

Engaging with the Student Learning Objectives (ESLO) Working Group Update
by Younggon Bae
Since its first meeting in October 2022, the ESLO working group has been meeting every other week in Fall 2022 and Spring 2023 to review the first version of Student Learning Outcomes (SLOs) documents. In the online group meetings, high school teachers and GeT instructors have shared their individual reactions to each SLO and discussed ways to improve the summaries and descriptions of the SLOs. Some ESLO group members attended the GeT Together and RUME Pre-Conference workshops on February 22-23 in Omaha, where they had a chance to meet the author team members and share their views on the current version of SLOs. As of April 2023, the group has reviewed SLOs 1 through 5 and started documenting written feedback for the author team. Additionally, some members of the ESLO group are contributing to book chapters.
Suggested Citation
Bae, Y. (2023, April). Engaging with the Student Learning Objectives (ESLO) Working Group Update. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#engaging-with-the-student-learning-objectives-eslo-working-group-update

Transformations Working Group Update
by Julia St. Goar
This spring, the transformation group is meeting every other Wednesday at 11:00 AM EDT and has been particularly focused on disseminating results. In February, several members of the transformation group presented a contributed paper titled “GeT Lesson Study: Engaging Prospective Teachers in Defining Mutuality” at the SIGMAA on RUME conference (Boyce et. al., 2023). Additionally, the group is working on writing two potential chapters for the upcoming handbook The GeT Course: Resources and Objectives for the Geometry Courses for Teachers. One potential chapter relates to ways in which transformation geometry can be axiomatized and brought into a GeT course in a rigorous way, while also being adaptive to the wide variety of contexts in which GeT courses are taught. The other potential chapter relates to the work presented at the RUME conference above, which focuses on a lesson featuring Adinkra originating from Ghana (Eglash et. al., n.d.) as well as concepts relating to transformation geometry. This semester, two members of the transformation group have further modified the “Adinkra” lesson and taught these modified lessons in their own classes. The group is engaging in further analysis of data collected from these and previous iterations of the lesson. Work on this “Adinkra” lesson has become such a significant focus that many members, under the leadership of Steven Boyce, have chosen to meet every-other-week, alternating with the “main” transformation meeting time, to have additional time to focus on work surrounding this lesson.
References
Boyce, S., An, T., Pyzdrowski, Oppong-Wadie, K., Ion, M., & St. Goar, J. (February, 2023). Learning from Lesson Study in the College Geometry Classroom. Proceedings of the 25th Annual Conference on Research on Undergraduate Mathematics Education. Omaha, NE. (To Appear)
Eglash, R., Bennet, A., Krishnamoorthy, M., Sawyer, S., & Adali, S. (n.d.) Adinkra Background. Culturally Situated Design Tools. https://csdt.org/culture/adinkra/index.html
Suggested Citation
St. Goar, J. (2023, April). Transformations Working Group Update. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#transformations-working-group-update

Teaching GeT Working Group Update
by Nathaniel Miller
The Teaching GeT group continues to be very busy! Most of us are working on different contributions for the upcoming book, and many of us got to work together in person in Omaha at the RUME conference in February. As a group we are discussing how to realize our vision of having the SLOs being a living document and how to make it possible for other people to propose modifications for them. We have also been discussing how to respond to some feedback that we have gotten from members of the ESLO group. As always, we would welcome more members, and if anyone has feedback about the SLOs that they would like to share with us, we would love to hear from you. Any inquiries, feedback, etc., can be sent to me at nathaniel.miller@unco.edu.
Suggested Citation
Miller, N. (2023, April). Teaching GeT Working Group Update. GeT: The News!, (4)2. https://www.gripumich.org/v4-i2-wi2023/#teaching-get-working-group-update

GeT to Know the Community
GeT: A Pencil community members and the GRIP Lab Staff at the GeT: Together at RUME meeting.

Top row (left to right): Laura Pyzdrowski (West Virginia University), Steve Boyce (Portland State University), Mara Markinson (Cuny Queens College), Tuyin An (Georgia Southern University), Dorin Dumitrascu (Adrian College), Sharon Vestal (South Dakota State University), Orly Buchbinder (University of New Hampshire), Carolyn Hetrick (University of Michigan), Inese Berzina-Pitcher (University of Michigan), Mike Ion (University of Michigan), Nat Miller (University Northern Colorado), Steve Szydlik (University of Wisconsin Oshkosh), Younggon Bae (The University of Texas Rio Grande Valley), Amanda Brown (University of Michigan)
Bottom row (left to right): Michaela Tracy (Lexington High School), Erin Krupa (North Carolina State University), Pat Herbst (University of Michigan), Henry Escaudro (Juniata College), Tabitha Mingus (Western Michigan University), Ruthmae Sears (University of Southern Florida)
Did you get promoted? Win a grant? Have a baby? Buy a house? We would love to feature your news, whether professional or personal! Email us at GRIP@umich.edu.

To submit a paper to be highlighted in a future newsletter, please fill out this form.
GeT Support
Sponsored by NSF DUE-1725837. All opinions are those of the authors and do not necessarily represent the views of the National Science Foundation or the University of Michigan.
Patricio Herbst, PI
Amanda Brown, Co-PI
Get Support is housed in the GRIP Lab at the University of Michigan
Inese Berzina Pitcher, Project Manager
