GeT: The News! Volume 6, Issue 1, Fall 2024

Table of Contents

GeT: A Pencil Community Flourishes with Recent Updates and Exciting Opportunities by Steven Boyce
Technology in GeT Courses by Tuyin An; Sharon Vestal; Erin Krupa; Orly Buchbinder
The Role of Angles and Angle Measure in a Transformations-based Approach to Geometry by Kevin M^cLeod
Using Polygons Card Sort Activity to Attend to Precision in Geometric Vocabulary and Concepts by Ruthmae Sears; Orly Buchbinder
Working Group Updates
Member Highlight – Interview with Irma Stevens!
Closing Notes
Upcoming Seminars
Future Community Gatherings

GeT: A Pencil Community Flourishes with Recent Updates and Exciting Opportunities

by Steven Boyce

This is a year of transitions for the GeT: A Pencil community. In May of 2024, project leaders Pat Herbst and Amanda Brown asked if Steve Syzdlik and I would assist with editorial duties for GeT: The News in the 2024-2025 academic year, working with Research Technician Anthony Davis. Our vision for the newsletter this year is that it will provide opportunities to engage, maintain, and expand our community. The GeT: A Pencil community is special because it brings together mathematicians, mathematics educators, teacher educators, and educational researchers from across the country to work together toward a shared goal: to productively impact the ways teachers become prepared to teach geometry. As you read this, I hope you believe that there is a place for you in our community. Whether you are an emeritus professor, a new instructor, or a teacher leader, your experiences and insights are welcomed!

In October, Hurricane Helene forced the cancellation of a Special Session of the American Mathematical Society Southeast Sectional Meeting in Savannah, Georgia focused on Geometry for Teachers courses. We extended invitations to community members whose sessions were canceled to write about their work in this newsletter instead. This issue of GeT: The News includes three articles by GeT community members, collectively addressing topics of technology, definitions, and transformations. In the first article, An, Buchbinder, and Krupa reflect on the current and potential role of technology in their GeT courses. In the second article, McLeod describes new insights on relationships between angle measure and angle definition and the choice of definition of rotation to support transformational proof. In the third article, Sears and Buchbinder discuss outcomes from a sorting activity (using technology) for teaching geometric definitions.

Working Groups for the GeT: A Pencil have been hugely impactful on me. I consider myself a “mid-career” mathematics educator, as I enter my 8th year teaching College Geometry courses.
I’ve been a member of the SLOs working group and the Transformations working group, and in both situations I’ve had the opportunity to deepen my Geometry Knowledge for Teaching and improve my teaching. This Fall, the GeT community started three new Working Groups. In this newsletter, the organizers for each Working Group summarize their current foci. The primary contact for each working group is available as well if you would like to learn more. I encourage you to check them out, particularly if you haven’t been part of a Working Group before.

Lastly, an important aspect of the newsletter is building our community and inviting new members. The newsletter closes with a shout out to our wonderful GeT Community members Stephen Szydlik and Dorin Dumitrascu. We also close with an introduction to a “returning” GeT member, Dr. Irma Stevens from the University of Rhode Island. Maybe next time we’ll GeT: to know more about you!

Technology in GeT Courses

by Tuyin An, Georgia Southern University; Sharon Vestal, South Dakota State University; Erin Krupa, North Carolina State University; Orly Buchbinder, University of New Hampshire

Technology is integral to modern education, supporting exploration, computation, assessment, communication, and motivation. National curriculum and teacher preparation standards, such as the Common Core State Standards for Mathematics (NGA & CCSSO, 2010) and Standards for Preparing Teachers of Mathematics (AMTE, 2017), emphasize the strategic use of technology in teaching mathematics across grade levels. At the college level, the Committee on the Undergraduate Programs in Mathematics recommends increasing the sophistication of technological tools used by mathematics major students (Zorn, 2015). The Mathematical Association of America Instructional Practices Guide views technology as a constant theme across instructional practices, promoting student engagement and learning (Abell et al., 2018).

As GeT instructors, our collaborative interest in technology emerged from our exploration of technologies such as Dynamic Geometry Environments (DGEs) and Digital Proof Tools (DPTs) in our teaching of geometry. We believe providing GeT students with initial exposure to technology tools can help them develop a positive attitude and appreciation for these tools and thus inspire them to incorporate such tools in their future classrooms. Our initial work on technology was the development of the narrative of SLO 6 – Technologies, calling for students to effectively use technology in GeT courses to explore, conjecture, and strengthen their understanding of geometric concepts and relationships. Working with DGE tools like GeoGebra, we observed how students naturally discovered geometric relationships through hands-on digital manipulation, while DPTs, like FullProof, could support both proof construction and proof evaluation with instant feedback (Baccaglini-Frank, 2011; Buchbinder et al., 2023; Bülbül & Güler, 2022). Combining research-informed practices and our own teaching experiences, we contributed a chapter on the topic of the importance and application of technology in GeT courses to the upcoming book entitled GeT Courses: Resources and Objectives for the Geometry Courses for Teachers. In the chapter, we further elaborated on SLO 6 and shared how DGE and DPT-incorporated activities could cultivate students’ geometric habits of minds (Driscoll, 2007) in various geometry contexts, such as proof writing, constructions, transformations, Euclidian and Non-Euclidian geometries.

Looking forward, we see tremendous potential in emerging technologies (e.g., generative AI and augmented reality). GeT instructors should stay updated on the latest technology trends and developments, be aware of potential challenges and solutions, and reflect on the use of technology in their teaching, in order to create supportive and engaging learning environments to foster students’ mathematical thinking.

References

Abell, M., Braddy, L., Ensley, D., Ludwig, L., & Soto-Johnson, H. (Eds.). (2017). MAA instructional practices guide. Mathematical Association of America. https://maa.org/resource/instructional-practices-guide/

Association of Mathematics Teacher Educators [AMTE]. (2017). Standards for preparing teachers of mathematics. https://amte.net/standards

Baccaglini-Frank, A. (2011). Abduction in generating conjectures in dynamic geometry through maintaining dragging. In Proceedings the 7th Conference on European Research in Mathematics Education (pp. 110-119).

Buchbinder, O., Vestal, S., & An, T. (2023). Lessons learned using FullProof, a digital proof platform, in a geometry for teachers course. Proceedings of the 25th meeting of the MAA special interest group on research in undergraduate mathematics education. Omaha: RUME.

Bülbül, B. Ö., & Güler, M. (2022). Examining the effect of dynamic geometry software on supporting geometric habits of mind: A qualitative inquiry. E-Learning and Digital Media, 20427530221107776.

Driscoll, M. J., DiMatteo, R. W., Nikula, J., & Egan, M. (2007). Fostering geometric thinking: A guide for teachers, grades 5-10. Heinemann.

National Governors Association Center for Best Practices [NGA] & Council of Chief State School Officers [CCSSO]. (2010). Common c ore s tate s tandards for m athematics. http://www.corestandards.org/Math/Zorn, P. (Ed.). (2015). 2015 CUPM curriculum guide to majors in the mathematical sciences. Mathematical Association of America.

The Role of Angles and Angle Measure in a Transformations-based Approach to Geometry

by Kevin M^cLeod, University of Wisconsin-Milwaukee

In this note, I would like to present one recurring issue that surfaced in the discussions of the GeT Transformation Geometry Working Group, and a partial resolution of that issue, contained in a suggestion by one of the reviewers of our chapter in the forthcoming GeT volume M^cLeod et al., in press). More details of the axioms involved can be found in Venema (2011) and M^cLeod et al. (in press).

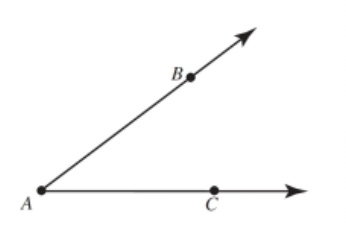
The issue in question was angle measure. For example, it is by two rays with a common endpoint. The figure therefore shows just one angle-although in my experience about half of all students will say it shows two-which presumably How many angles in this figure? therefore has just one measure. As group members pointed out, however, it is a common practice to refer to both interior and exterior measures of the angle. Other questions arose as to the range of possible angle measures: some group members allowed only angle measures between 0^◦and 180^◦; some allowed angle measures up to 360^◦; some allowed negative angle measures to describe clockwise rotations, as is routinely done in trigonometry. An additional recurring issue was that of distinguishing between the measure of an angle, and the measure of an amount of turn.

In a typical transformations-based approach to geometry, the SAS Triangle Congruence Postulate is demoted from the status of an axiom, and is replaced by one or more axioms stating the existence and properties of certain classes of distance-preserving transformations. For example, Venema (2011, Chapter 10) proposes a reflection axiom:

(The Reflection Postulate) For every line ℓ, there exists a function ρ_l from the plane to itself, called the reflection across ℓ, which satisfies the following conditions:

If P lies on ℓ then ρ_ℓ(P) = P;
If P lies in one of the half-planes bounded by ℓ then ρ_ℓ(P) lies in the opposite half-plane;
ρ_ℓtakes lines to lines;
ρ_ℓpreserves distances and angle measures.

We note that the transformations mentioned in the Common Core State Standards for Mathematics (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010) include translations, rotations, and reflections, but since translations and reflections can be constructed as compositions of reflections, an axiom for reflections is logically sufficient. For pedagogical reasons, however, one might choose to have separate axioms for translations and reflections, as we did in our chapter. In the original submission of our manuscript, we included the following version of the Rotation Postulate:

(The Rotation Postulate, initial version) For every point C, and every real number r with 0 < r < 180, there exists a function R_r,Cfrom the plane to itself, called the rotation about C through r^◦, which satisfies the following conditions:

R_r,C(C) = C;
If P ≠ C then R_r,C(P) = P^′, where P^′C = P C, m(∠P CP^′) = r^◦, and the shorter direction from P to P^′around the circle with center C and radius CP is measured counter-clockwise;
R_r,Ctakes lines to lines;
R_r,Cpreserves distances and angle measures.

The reviewer pointed out that ‘It’s a bit ungainly that the Rotation Postulate refers to angle measure whereas the translation postulate does not refer to distance measure,’ and suggested a modification of the Rotation Postulate, which led to the final version in our chapter:

(The Rotation Postulate, final version) For every point C, and every pair of distinct rays r and r^′with common endpoint C, there exists a function R_C,r,r′ from the plane to itself, called a rotation around C, which satisfies the following conditions:

R_C,r,r′(C) = C;
If P ≠ C, then R_C,r,r′(P) ≠ P;
R_C,r,r′ takes r to r^′;
R_C,r,r′ takes lines to lines;
R_C,r,r′ preserves distances and angle measures.

Not only does this version of the postulate make no reference to angle measure, or the amount of turn, it also does not mention the direction of rotation. In this, it is much more akin to the modern idea of a transformation as a mapping, or function, from the plane to itself, rather than an actual ‘rigid motion’.

The reader may find it interesting to prove the SAS congruence criterion, using transformation axioms. Some questions:

Can you prove the SAS criterion using only the Reflection Axiom?
What advantages do you see to having axioms for all three types of rigid motion? In particular, does this extra flexibility allow for easier, or pedagogically preferable, proofs of SAS?
What advantages do you see to the final version of the Rotation Postulate over the earlier version
(Extra credit!) Where else might one de-emphasize angle measure, if one takes a resolutely transformational approach to high school geometry?

References

[1] M^cLeod, K., Sears, R., Lai, Y., St Goar, J. & Prasad, P.V. (to appear). Promoting rigor and proof via a transformations-based approach for isometries-based lessons in the Geometry for Teachers course, in The GeT Course: Resources and Objectives for the Geometry Course for Teachers.

[2] National Governors Association Center for Best Practices [NGA], & Council of Chief
State School Officers [CCSSO]. (2010). Common core state standards for mathematics.
Available at https://www.thecorestandards.org/Math/

[3] Venema, G. A. (2011). Foundations of Geometry. (2nd ed.) Pearson.

Using Polygons Card Sort Activity to Attend to Precision in Geometric Vocabulary and Concepts

by Ruthmae Sears, University of South Florida; Orly Buchbinder, University of New Hampshire

Technological tools can be used in teacher preparation programs to develop students’ conceptual understanding of the properties of polygons and to communicate appropriate vocabulary (Kartal & Çınar, 2024). The exploration opportunities afforded using technological tools, such as Desmos, can help students develop conceptions of shapes, engage in informal deduction, and enhance their mathematical vocabulary (Herman, 2022). This article describes how graduate students in a mathematics education teacher preparation program engaged in a card sort exercise to describe properties of polygons using a Desmos activity (https://teacher.desmos.com/activitybuilder/custom/67224d9437c8fd0a42d4c764).

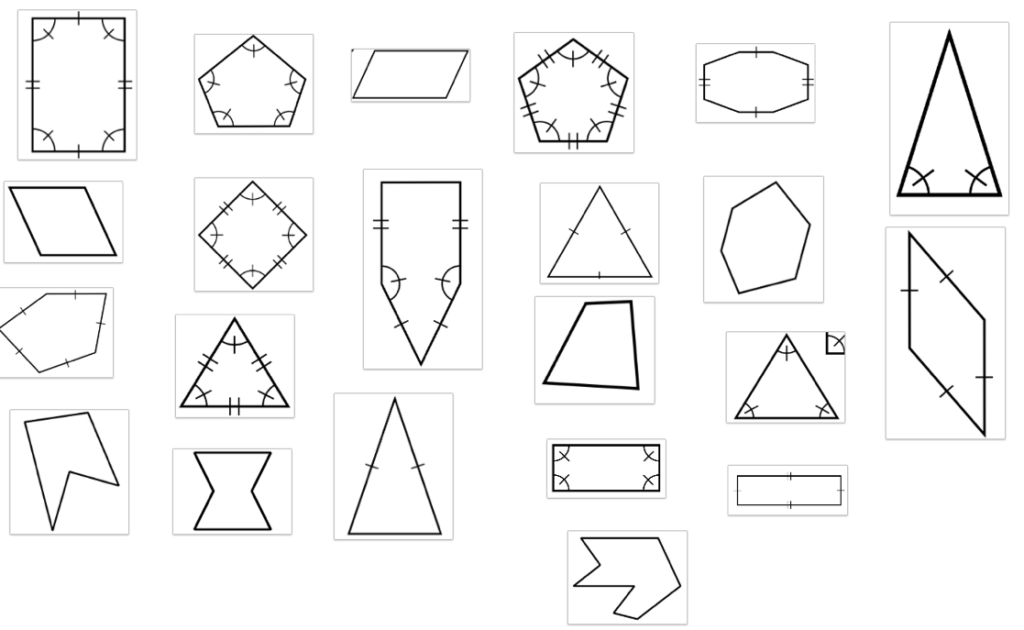
The data were collected in Spring 2024 from four students at a university located in the southeastern region of the United States. The students were assigned to complete a polygon card sort activity, which was designed to develop their geometric vocabulary and incorporate the following terms: convex, concave, regular, equiangular, and equilateral (Brown, n.d.). Particularly, the students were asked to sort the polygons in Figure 1 using their preferred grouping criteria and to explain the rationale for their grouping. They were then asked to sort the same cards using different grouping criteria and to provide reasoning. Afterward, the students were presented with sorted polygons as “convex,” “concave,” “equilateral,” “not equilateral,” “equiangular,” “not equiangular,” “regular,” and “not regular polygons,” and students were asked to provide an explanation of what the terms “convex,” “concave,” and “regular” meant (Brown, n.d).

Figure 1. Polygons in card sort activity (Brown, n.d.).

This activity was rich in having students consider the properties of polygons as it helped strengthen their vocabulary of geometrical concepts. However, the students struggled to use proper terminology to justify their thoughts and explain their thinking robustly. For instance, during the first sorting attempt, the students grouped the polygons based on the number of sides or by the mere presence of the markings on the polygons. Interestingly, the students did not attend to the symbolic meaning of these markings as representing equiangular or equilateral properties. Instead, students referred to the presence and positioning of the markings on sides or angles. This suggests a superficial sorting that does not attend to the properties of polygons but only to the perceptual features of the diagrams. For instance, for Figure 2, Student A indicated:

“The first group I made was all the triangles. Then, I combined all the pentagons. Next, I grouped together any polygon with greater than 5 sides. Lastly, I split the quadrilaterals between two groups. One group is any quadrilateral with congruent sides or angles. The other group is any quadrilateral without congruent markings.”

Figure 2. Student A’s first grouping

In a similar fashion, Student B explained that they sorted the polygons based on the visual clues:

“I sorted by grouping:
– All shapes that have all information given (sides, angles)
– shapes that have only information about the angles
– shapes with no given information
– shapes with only information on the sides
– shapes with some information given”

Figure 3. Student B’s work on the first grouping.

These examples show that the vocabulary utilized by students for justifying their first polygon sorting was limited. It avoided descriptive phrases and mathematical terminologies that attend to the geometric features and properties of polygons, as the task intended. This suggests that in this first sorting, the students were operating at level 1 (visualization) of the van Hiele Model of Geometrical Thought (Armah et al, 2018) because they focused primarily on visualization, with minimal progress in the analysis level of classifying shapes by their properties.

For the second grouping, there was a slight improvement in the usage of geometrical terms. As an example, Student C indicated that,

“First, I made the grouping of convex polygons with no given angles or congruent sides. Second, I classified concave polygons. Next, I grouped any polygon with only congruent sides. Then, I added a class for both all congruent sides and angles (partial definition of triangle, square, and pentagon). Lastly, I grouped full definitions of a triangle, square, rectangle, and pentagon).”

Figure 4. Student C’s work on the second grouping.

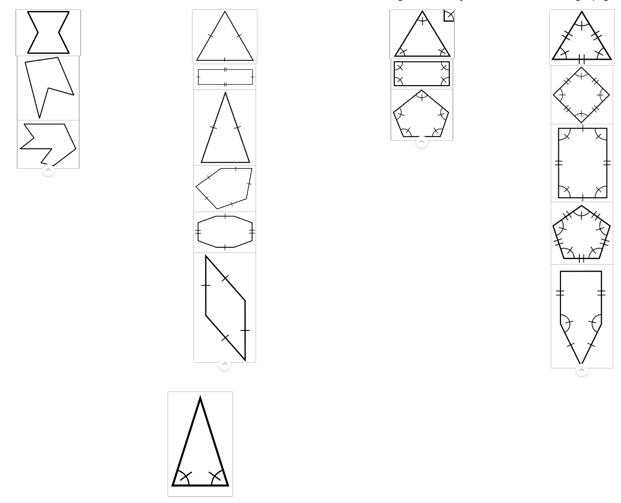
In this response, we observe the use of geometry vocabulary (concave, convex, congruent) as well as some polygon names. The vague term “partial definition” was interpreted as an improper attempt to refer to features of regular polygons, which are both equiangular and equilateral. Student’s C grouping of information by either sides or angles was conveyed as “partial definition,” whereas, the presence of marking of both angles and sides was referred to as “full definition.” This (mis)use of the terms suggests a fragile conception of polygons and their properties.

When students were given the sorted polygons grouped by specific geometric categories, they were asked to explain the meaning of certain terms, like concave and convex. Student A wrote: “Concave polygons represent those that ‘cave’ inwards to the interior of the shape. The convex polygons do not have this aspect.” While this way of thinking can be helpful as a mnemonic device to recall or help students recall the term “concave,” it would be valuable if the student would be able to provide a more precise mathematical definition of “concave,” although not necessarily a formal definition. Student C came closer to using the definition of “concave,” while still making an imprecise claim, saying: “The convex polygons have no line containing a side that has a point within the interior of the figure while concave (non-convex) polygons do have at least one line that passes within the interior.” A more precise definition for a convex polygon is that every segment connecting two points within the polygon lies entirely within the polygon. There seems to be an attempt to use proper mathematical vocabulary. However, the terms are not appropriately defined.

Some definitions seem easier for students to explain. For example, to define equiangular and equilateral with a great degree of precision, Student A noted: “Equilateral means that all of the sides in the polygon are congruent to each other. Equiangular means that all of the angles in the polygon are congruent to each other.” This comes closer to van Hiele level 2 (analysis). Given that the van Hiele model of geometrical thinking suggests that individuals learn geometry across five levels (visualization (level 1), analysis (level 2), abstraction (level 3), deduction (level 4), and rigor (level 5)) it appears that the depth of knowledge exhibited were generally rudimentary.

Following this activity, an instructor (the first author of this paper) engaged students in a rich mathematical discussion, helping them clarify the meaning of geometric terms and use proper vocabulary. Additionally, the students engaged in didactical discourse around the implications of attending to precision by both teachers and students in geometry classrooms. The students were encouraged to reflect on their responses from a teacher’s perspective and provide pedagogical recommendations to enhance the description of the groupings and deepen their geometrical understanding. This strategy aligns with Student Learning Objective 3 (SLO-3) (Get: A Pencil, 2022), which suggests that “Future secondary geometry teachers must deeply understand specialized content that is aligned to national and state secondary standards, know the best practices for teaching the content, and be able to reflect on their teaching.”

The ways in which future teachers and graduate students define terms have implications for their abilities to communicate and conceptualize a geometric concept, reason, and produce proofs. Thus, attention is needed to develop their geometric vocabulary. The results suggest that the students struggled to provide detailed descriptions to justify their grouping of polygons. GeT course instructors should attend to students’ development of geometrical understanding progression and provide opportunities for students to advance across van Hiele levels of Geometric Thought.

References

Armah, R. B., Cofie, P. O., & Okpoti, C. A. (2018). Investigating the effect of van Hiele phase-based instruction on pre-service teachers’ geometric thinking. International journal of Research in Education and Science, 4(1), 314-330.

Brown, R. Polygons Card Sort. https://teacher.desmos.com/activitybuilder/custom/67224d9437c8fd0a42d4c764

Get: A Pencil: Student Learning Objective 3 (SLO 3). – Secondary geometry understanding. https://getapencil.org/learning-objective-3/#summary

Kartal, B., & Çınar, C. (2024). Preservice mathematics teachers’ TPACK development when they are teaching polygons with GeoGebra. International Journal of Mathematical Education in Science and Technology, 55(5), 1171-1203.

Herman, T., Suryadi, D., & Prabawanto, S. (2022). Concept of polygon: Case study of elementary students’ difficulties. Mathematics Teaching Research Journal, 14(5), 34-47.

Working Group Updates

Focus: SLO 9 and SLO 4 (tangentially)

The Wednesday GeT Working Group has been discussing SLO 9: Non-Euclidean Geometry and SLO 4: Axioms & Models. The group consists of five community members (S. Greenwald, R. Bell, T. Mingus, D. Dumitrascu, and K-H. Roh). We are working towards common goals of (1) creating activities (to be published open-access) for the community and (2) revisiting the SLOs on a deeper level. We met three times this semester, once to organize and twice to respond to specific prompts. In our November meeting, we shared the topics and activities that we use when we first introduce GeT students to non-Euclidean geometries. In our December meeting, we shared how we communicate to future geometry teachers the reasons why we study non-Euclidean geometries and why the study of such geometries is important. We are next scheduled to meet on January 15, 2025.

Please reach out to the facilitator, Bob Bell (bellro@msu.edu), for more information.

Focus: SLO 9 and SLO 4

In fall 2024, we convened the Thursday Working Group on the third Thursday of every month. This group is composed of pure mathematicians, mathematics teacher educators, and high school mathematics teachers. We are building on the work of the ESLO group, which met over the 2022-2023 and 2023-2024 academic years to first read and provide commentary on each of the ten SLOs, and then propose and examine geometry tasks specifically targeting SLO 3. This collection of tasks was saved in an online folder and is serving as an instructional resource for the members of the group. This year’s group is primarily focused on SLO 6, and is revisiting each of the tasks proposed and analyzed by the ESLO group from an “SLO-6 lens”. For each task, we are discussing ways to implement the use of dynamic geometry environments and, when applicable, digital proof tools. For our first meeting, we discussed the Midpoint Quadrilateral Task which leads to Varignon’s Theorem and for our next meeting, we will discuss a paper folding reflections task. Our group is always open to new members – reach out to the facilitator, Mara Markinson (mara.markinson@qc.cuny.edu), for more information.

Focus: SLO 8 (construction) along with SLO 1 (proof)

Our working group meets bi-weekly on Friday afternoons from 2-3 PM. Due to the availability of our group members, our working group has met twice so far and will meet one more time by the end of this semester. During the first two meetings, we established the focus of the group: geometry constructions (SLO8) along with proofs (SLO1).

We have set the following tasks for the rest of this semester: gather resources related to geometric constructions (articles, books, websites, tools, etc.), and brainstorm a possible scholarly product to support our publication needs. Additionally, we attended Dr. McDaniel’s GeT seminar in November to learn more about his construction-focused work.

Starting as a relatively small group, we aimed to expand our membership to include more expertise. We reached out to a few GeT community members who we know have a passion and expertise in geometry constructions and invited them to join us. We are now a group of six members (listed alphabetically): Tuyin An, Erin Krupa, Michael McDaniel, Nathaniel Miller, Laura Pyzdrowski, and Steve Szydlik (who will join us next semester). We are hopeful to establish more concrete goals in our next meeting this month. The meeting time is Dec. 13 from 2-3 PM. We will resume our group meetings next semester in January. Anyone interested in this topic is welcome to join us!

Please reach out to the facilitator, Tuyin An (tan@georgiasouthern.edu), for more information.

Winter 2024 – Transformation Group Update

In the summer and fall of 2024, the transformation group mainly focused on creating a sequence of lessons that GeT instructors could insert into their course to teach the proof of the Side-Angle-Side (SAS) triangle congruence criterion from a transformation perspective. Work on this front has proceeded in several ways. First, the transformation group reviewed several ways that the SAS proof could be written, especially based on the axiomatic structure and context of the course. The initial goal here was to select one axiomatic structure and proof approach that our lesson sequence would focus on, but since then the group has settled on the idea of creating at least two versions of the lesson plan that would accommodate some of the different ways of structuring previous properties and axioms. Second, the transformation group has worked on viewing different ways instructors and various sources have taught the SAS proof and some of the background material in these contexts. One interesting concern that came up here was that some instructors made extensive use of technology, while others indicated they wouldn’t reasonably be able to incorporate a lesson with such significant technology without extending the length of the sequence of lessons. Currently, a version of the lesson that doesn’t involve technology is more extensively developed, but the group plans to look into ways to incorporate more technology, either as a separate version of the lesson or as one that accommodates a variety of needs.

This semester, Kevin McLeod is incorporating a version of the SAS lesson sequence into his GeT course, so the group will discuss how this iteration of the lesson went for the purposes of modifying the SAS sequence. The group plans to work to accommodate further instructors in the group who may be interested in incorporating a version of the lesson sequence into their GeT courses as well. Furthermore, group members have been writing reflections after each meeting so that the group can later take a broader look at how the process of collaborating to create the SAS lesson sequence has gone.

In the upcoming semester, we plan to continue the above-described directions of work.

Please reach out to the facilitator, Julia StGoar (stgoarj@merrimack.edu), for more information.

Member Highlight – Interview with Irma Stevens!

What is special about your GeT course? In 2-3 sentences, describe your GeT course

I chose to let my students from this semester respond to these questions. Here, unfiltered, is what my students from this semester shared about the course:

Our class is not directed as much by direct instruction, but rather by rich discussion. Understanding is achieved by communication, and our many different backgrounds lead to so many unique perspectives. Geometry can easily be viewed both theoretically and applicably, meaning many students can find ground to stand on.

class structure isn’t stressful in the way many other mathematics classes are: furthermore Dr. Stevens expertly breaks down precisely key elements of geometry; insofar as In-Class and Homework material is never frivolous, even upon immediate inspection.

It’s a very interesting deep dive into the foundations of geometry. We cover much of high school geometry and expand on many ideas or prove different things that you don’t usually cover in high school math.

It’s a lot of group work and working problems out. It’s nice that there’s a final project and not a final exam. it’s a small class, which is nice cause you really get to know how each person works so you know who you work best with.

The amount of collaboration that Professor Stevens fosters in our class. Typical math lessons have us sit down for hours in our seats listening to the expert teach of hours. She makes us step into the shoes of the experts for a bit and creatively solve problems we’ve never seen before.

Who are your students?

Here is how some of my students from this semester describe themselves:

We are a wide range of students, from sophomores to seniors (maybe even grad students?) with an interest in math. Whether pure or applied, or paired with computer science or engineering or education, our differing experiences make for a very diverse learning environment.

I am a 4th year undergraduate going for a Bachelor of Sciences Degree for Mathematics

I am a Computer Science and Applied Mathematics double major hoping to go into the field of Audio Engineering

Math majors, and other degrees that deal heavily with math.

Curious explorers, charting the voyage of the discovery of the universe.

What are you most interested in learning/achieving through participating with the GeT: A Pencil community?

This one, I can answer. I am most interested in learning about new research-based ideas for lessons, reflecting on my teaching, challenging my own perspectives on what it means to teach a GeT course, and supporting other instructors in doing the same. The main ways I have done so thus far is via the alignment of the SLOs to my course and the co-design, implementation, and collaborative reflection of the Adinkra lesson (thank you, Adinkra Lesson group!).

What is your favorite book you have read in the last few years?

Hello Beautiful by Ann Napolitano- a lighthearted homage to Mary Alcott’s Little Women.

Here are what some of my students shared:
I don’t read books for fun, high school ruined reading for me
The Martian
And Then There Were None – Agatha Christie
Trapped in time by Evangeline Anderson

The Spy, Paolo Coehlo

Closing Notes

GeT: Book Shout Out

Before we close out this issue, we want to share a special shout out to Dorin Dumitrascu and Stephen Szydlik for their incredible work on the GeT Book. In particular, their work formatting chapters in LaTeX was incredibly helpful! The work and effort related to the GeT Book are truly appreciated!

Upcoming Seminars

We have had an exciting semester of incredible GeT Seminar Presentations. The GeT Seminar presentations provide an opportunity to learn about the great work members of our community have done. Over this last semester, we have heard from:

Presenter(s): Mara P. Markinson

Seminar Topic: How does an instructor of the Geometry for Teachers (GeT) course build a “thinking” geometry classroom?